Force Directed Method에 관한 게시물은 Universität Trier의 Philipp Kindermann 교수 강의를 바탕으로 작성하였습니다.
Visualization of Graph
데이터는 다양한 형태 및 특성을 가지고 있습니다. 특정 데이터셋은 Graph로 표현하는 것이 그 특성을 표현하는데 있어서 유리합니다. 예를 들어 나의 인간 관계를 데이터로 표현해야한다면 어떻게 표현하는 것이 가장 좋을까요? Graph 형태로 나의 인간 관계를 표현 하는것이 가장 직관적인 방법일 수 있습니다.
어떻게 Graph를 가장 직관적으로 잘 표현할 수 있을까요? 아래 그림에서 알 수 있듯이 같은 데이터지만 왼쪽보다는 오른쪽이 훨씬 더 직관적입니다. 이렇듯 Graph의 Node와 Edge를 직관적으로 잘 표현하는 방법 중 하나가 Force Directed Method입니다.
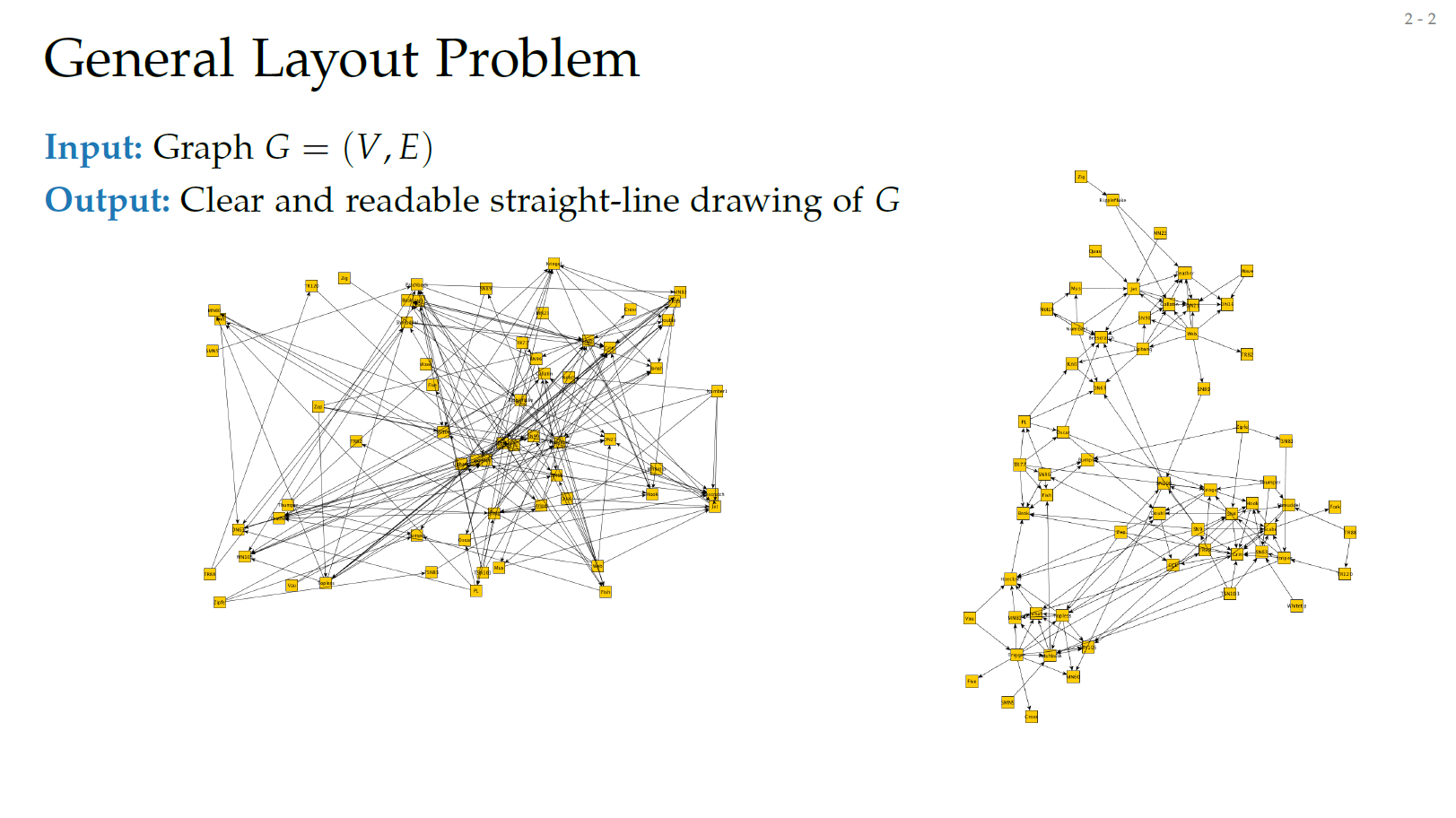
General Graph Visualization Problem
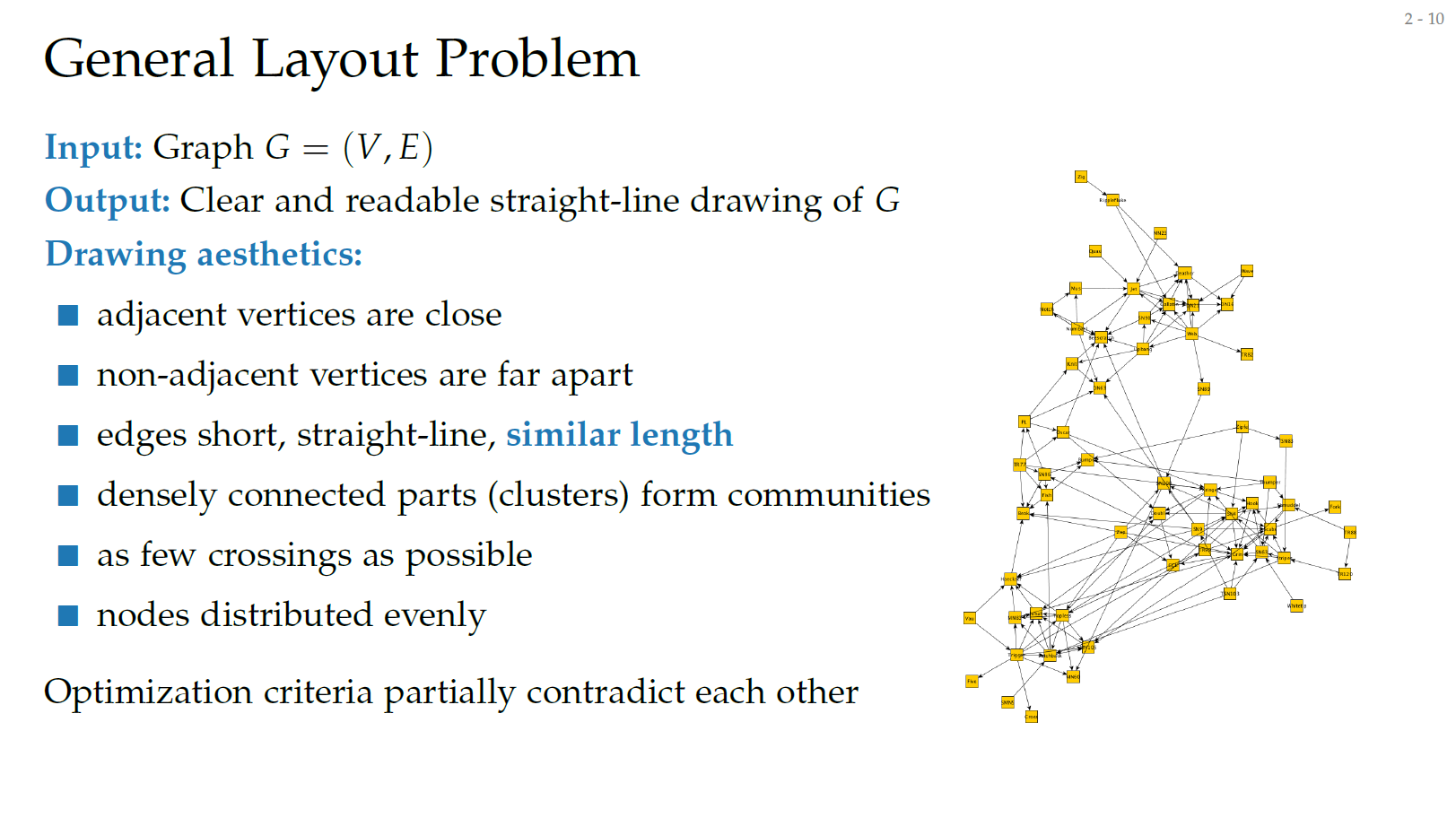
잘 표현한 Graph Visualization은 무엇이며, 그렇게 하기 위해서 어떻게 구현해야 하는가?
Graph의 직관적인 표현을 위해서는 몇가지의 기준이 있다.
- 연결된 노드들은 근접하게 위치할 것
- 연결되지 않은 노드들은 최대한 멀리 위치할 것
- 연결 노드간의 연결선은 최대한 짧고 직선일 것
- 밀접하게 연결되는 노드들은 하나의 군집을 형성할 것
- 가능한 노드 간 연결성은 교차되지 않도록 할 것
- 노드의 분포는 최대한 균일할 것
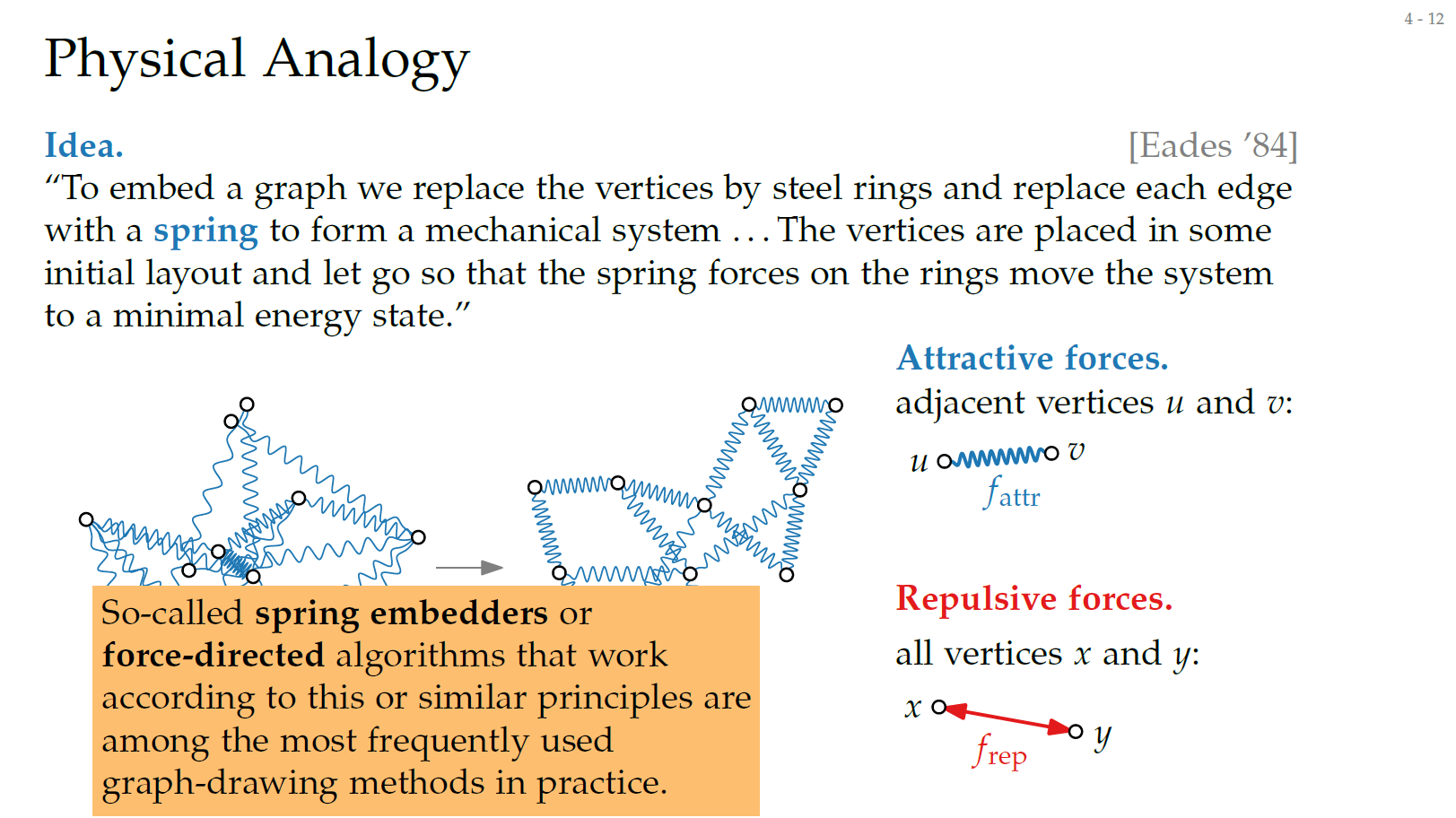
Force Directed Algorithm
Graph를 잘 표현하기 위한 기준을 만족하기 위한 알고리즘의 아이디어는 스프링이다! 예를 들어, 두 지점을 탄성이 있는 스프링으로 연결했다고 가정을 해보자. 만약 이 두 지점이 멀리 떨어져 있다면 스프링에 의해서 끌어당겨지는 힘(Attractive forces)가 가해져 서로 가까이 붙을 것 이다. 반대로 너무 가까이 있다면 오히려 반대로 밀어내는 힘(Repulsive forces)가 가해져 서로 멀어질 것이다. 결국에는 스프링으로 연결된 두 지점이 가장 안정적인 상태(Minimal energy state)에 도달하게 될 것이다.
이 간단한 원리를 적용하면 우리가 원하는 Graph를 잘 표현할 수 있는 알고리즘의 초석으로 활용할 수 있다. Force Directed Algorithm의 Pseudo Code는 아래와 같이 표현할 수 있다. 여기서 중요하게 봐야할 점은 Repulsive force는 선택된 vertice 외의 모든 vertices와의 $f_{rep}$ 를 계산하지만 Attractive force는 선택된 vertice와 edge 정보에 따라서 연결된 vertices들에 대해서만 $f_{attr}$ 을 구한다.

Pseudo Code의 Attractive Force와 Repulsive Force는 아래와 같이 구할 수 있다.

Attractive Force와 Repulsive Force의 특징을 살펴보면 아래의 그림과 같다. $f_{rep}$의 경우에는 두 vertice 사이에 어느정도 거리가 있다면 그 값이 0에 수렴하는 형태를 보여 힘이 거의 작용하지 않는 상태이며, ideal spring length인 $l$보다 거리가 가깝다면 $f_{rep}$가 커져서 두 vertice 사이의 거리가 멀어지는 힘이 작용한다. 반면 $f_{attr}$은 두 vertice 사이에 어느정도 거리가 있다면 서로 당기는 힘이 커지는 방향으로 작용한다.

References
[1] https://www.youtube.com/watch?v=WWm-g2nLHds
[2] https://cs.brown.edu/people/rtamassi/gdhandbook/chapters/force-directed.pdf