KL Divergence는 무엇인가?
Kullback-Leibler divergence(KL Divergence)는 하나의 확률분포로부터 다른 하나의 확률분포가 얼마나 다른지를 정량화한다.
Bayesian theory에서 true distribution $P(X)$가 있을 때, 우리는 $P(X)$를 approximate distribution인 $Q(X)$로 추정하고자 한다. 이런 경우, 우리는 KL Divergence를 이용하여 approximate distribution $Q(X)$와 true distribution인 $P(X)$의 차이를 정량화할 수 있다.
수학적으로 두 확률 분포함수 $P$, $Q$가 sample space $X$에 있을 때 KL Divergence는 아래와 같다.
\[\begin{align} D_{KL}(P \| Q)&=\mathbb{E}_{x \backsim P}[log(\frac{P(X)}{Q(X)})] \\ &= \int P(x)log(\frac{P(x)}{Q(x)}) dx & \text{for continuous random variable} \\ &= \sum P_i(x)log(\frac{P_i(x)}{Q_i(x)}) & \text{for discrete random variable} \end{align}\]KL Divergence의 특징
KL Divergence는 두 가지의 특징이 있습니다.
첫번재는 symmetric하지 않다는것입니다. 즉, $D_{KL}(P|Q) \not = D_{KL}(Q|P)$입니다. 따라서 KL Divergence는 거리의 개념이 아니다.
두번째는 KL Divergence의 값은 $[0,\infty)$의 값을 가집니다. 만약 두 분포가 같다면 KL 값이 0이다$(P=Q)$. 반면 point $x$에서 $Q(X)=0$이고 $P(X)>0$인 $x$가 존재한다면 KL 값은 $\infty$이다.
Forward and Reverse KL Divergence
만약 true distribution인 $P(X)$가 있고 approximate distribution $Q_{\theta}(X)$로 $P(X)$를 추정해보자. 그 방법으로는, Objective function을 통해서 $Q_{\theta}$를 update하여 $P(X)$를 근사할 수 있도록 최적화할 것이다.
KL Divergence의 특징에서 말한것처럼 KL Divergence는 symmetric하지 않다. 즉, $D_{KL}(P | Q) \not= D_{KL}(Q|P)$이다. 따라서 우리는 true distribution $P(X)$를 근사하기 위해 두 가지의 objective function을 생각할 수 있다.
\[\begin{align} 1) \text{ Minimizing the Forward KL: } \underset{\theta}{\operatorname{argmin}}(D_{KL}(P\|Q_{\theta}) \\ 2) \text{ Minimizing the Reverse KL: } \underset{\theta}{\operatorname{argmin}}(D_{KL}(Q_{\theta}\|P)) \end{align}\]Objective function Forward KL과 Reverse KL의 차이를 알아보기 위해 아래와 같이 가정한다. true distribution $P(X)$는 아래 그림과 같이 bimodal distribution이고 approximate distribution는 normal distribution $Q(X)=\mathcal{N}(\mu,\,\sigma^{2})\,$이다.
Forward KL: Mean-Seeking Behavior
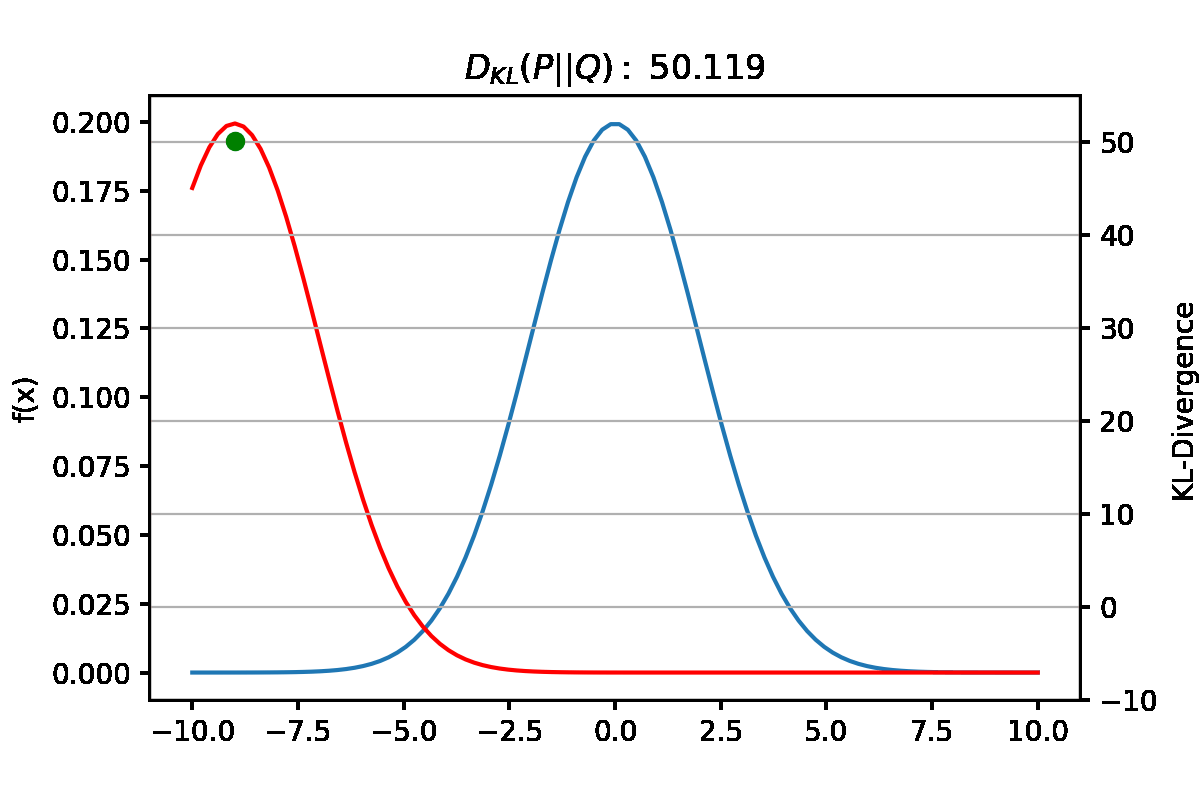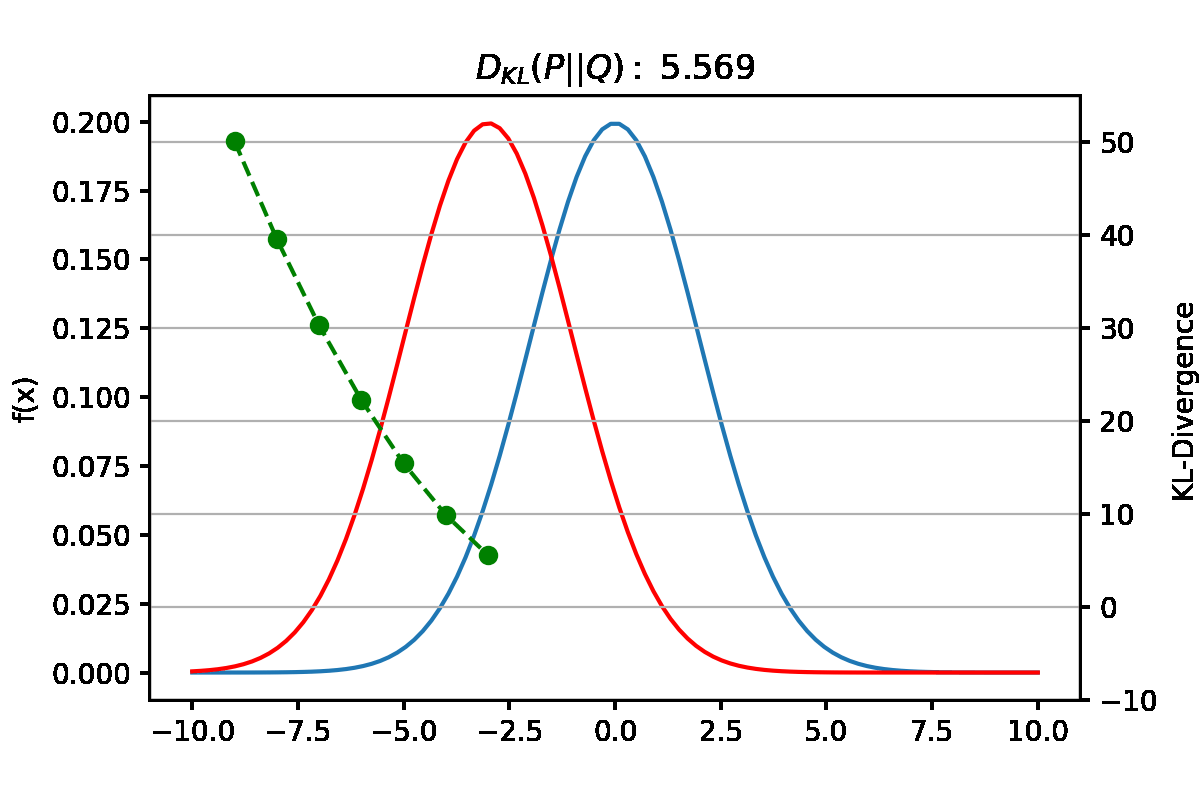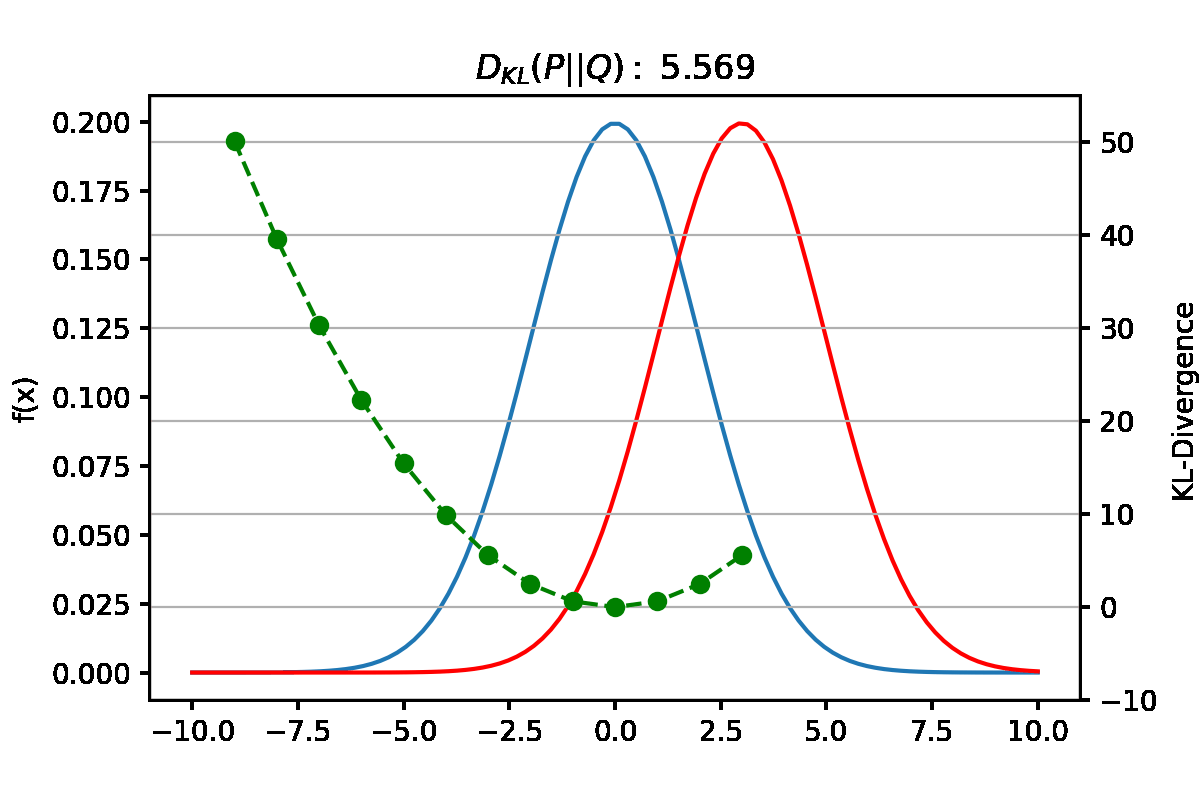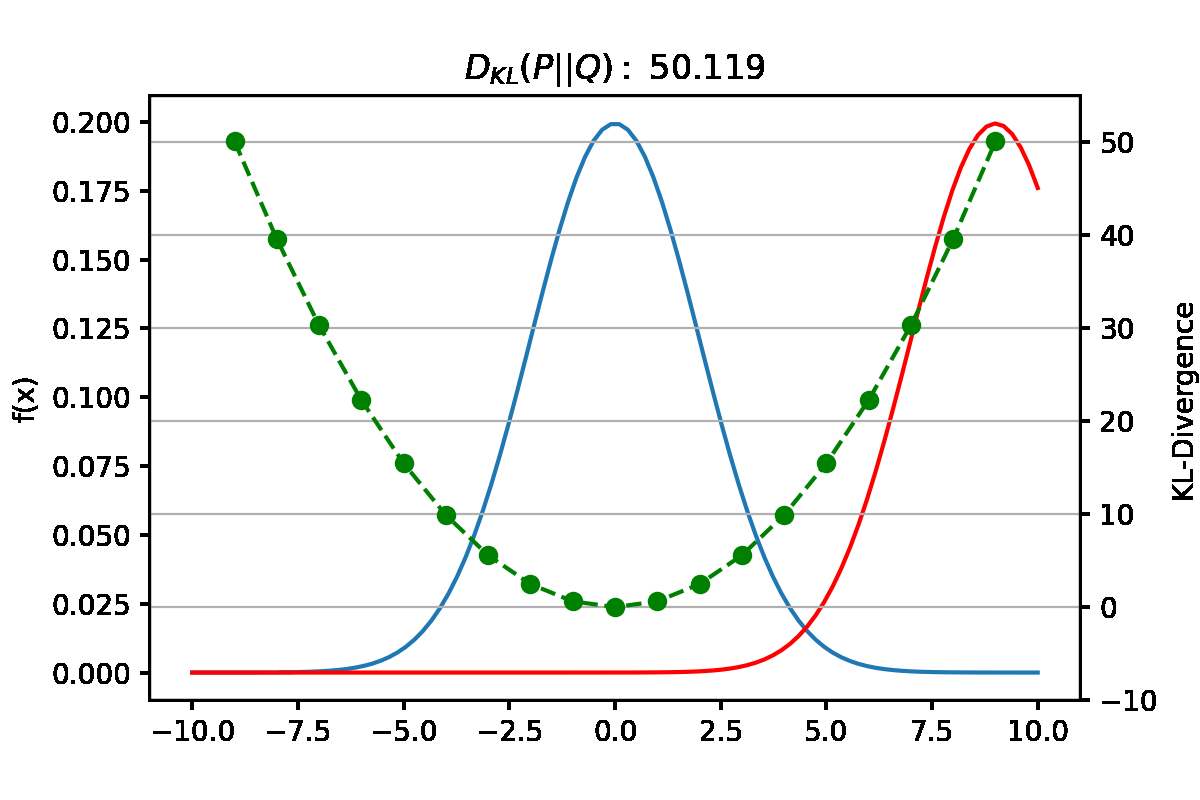
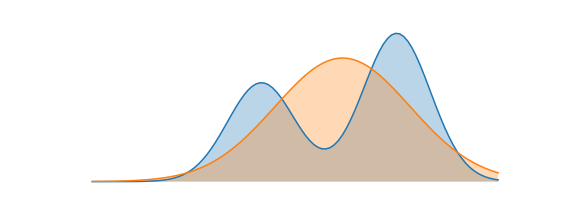
만약 $Q_{\theta}$의 Objective function을 Forward KL로 설정했다고 생각해보자. Forward KL은 식(4)와 같이 $P(x)$와 $Q(x)$의 차이를 $P(x)$로 weighted한 값이다. \(\begin{align} D_{KL}(P\|Q) = \sum P_i(x)log(\frac{P_i(x)}{Q_i(x)}) \end{align}\) $P(x)=0$인 x를 가정해보면, weight로 작용하는 $P(x)$가 0이므로 $P(x)$와 $Q(x)$의 차이와 무관하게 KL 값이 0이된다. 따라서 approximate distribution인 $Q(x)$은 무시된다고 볼 수 있다.
그렇다면, $P(x)>0$인 x는 어떤가? weight인 $P(x)$가 0보다 크므로 $log(\frac{P(x)}{Q(x)})$ term이 KL 값에 관여한다. Forward KL의 Optimization과정에서는 $P(x)$와 $Q(x)$의 차이를 나타내는 $log(\frac{P(x)}{Q(x)})$를 전체적으로 minimize하는 방향으로 될 것이다.
Reverse KL: Mode-Seeking Behavior
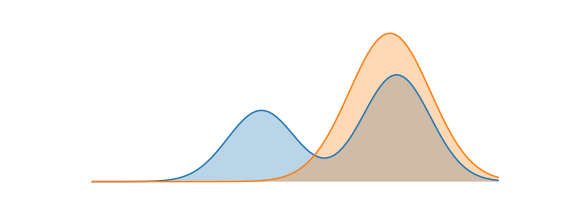
만약 $Q_{\theta}$의 Objective function을 Reverse KL로 설정한다면 어떨까? Reverse KL은 식(5)와 같이 $P(x)$와 $Q(x)$의 차이를 $Q(x)$로 weighted한 값이다. \(\begin{align} D_{KL}(Q\|P) = \sum Q_i(x)log(\frac{Q_i(x)}{P_i(x)}) \end{align}\)
Foward KL과 유사하게 weight인 $Q(x)=0$인 x에서는 $P(x)$와 $Q(x)$의 차이와 무관하게 KL 값이 0이된다. 따라서 approximate distribution인 $Q(x)가 0인 부분은 KL값이 0이므로 KL을 minimize할 때 상관하지 않아도 된다.
Reverse KL에서는 $Q(X)>0$인 곳에서 $P(x)$와 $Q(x)$의 차이를 얼마나 줄이느냐가 관건이다. bimodal distribution인 $P(x)$에서 좌우 mode를 다 잘 맞추는건 $Q(x)$의 가정인 normal distribution으로 힘들기 때문에, $P(x)$에서 더 dominant한 mode인 오른쪽 mode에 집중하여 가장 잘 맞추는 approximate distribution $Q(x)$가 되도록 하는것이 KL값을 minimize하는 방법이다.
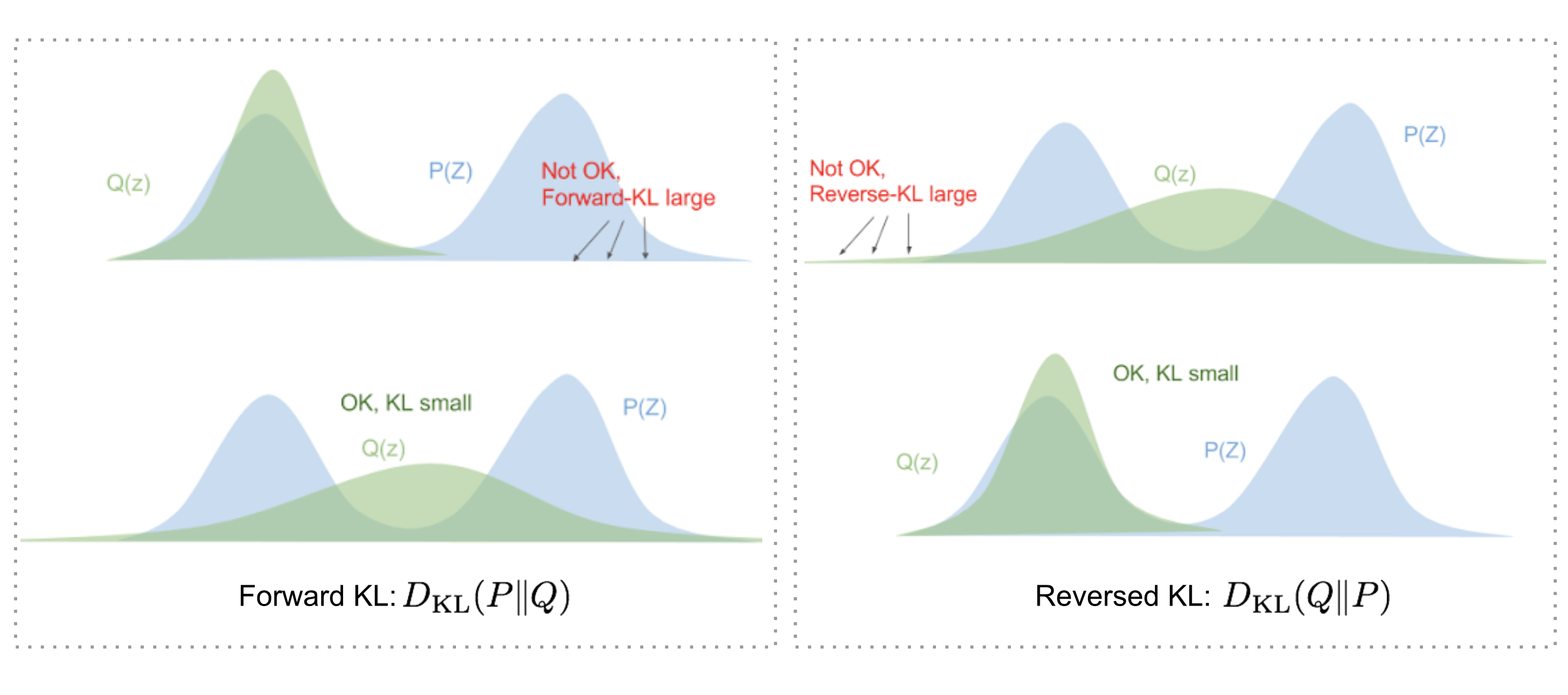
Forward KL과 Reverse KL 요약
References
[1] https://dibyaghosh.com/blog/probability/kldivergence.html
[2] https://velog.io/@tobigs-gm1/Variational-Autoencoder
[3] https://hyunw.kim/blog/2017/10/27/KL_divergence.html
[4] https://agustinus.kristia.de/techblog/2016/12/21/forward-reverse-kl/
[5] https://lilianweng.github.io/posts/2018-08-12-vae/