
Incremental Implementation이 뭔가?
행동의 가치(Action-value Methods)를 추정하는 방법에 대해서 우리는 관측된 보상의 표본 평균으로 가치를 추정했다.
Incremental Implementation은 행동의 가치 추정치인 관측된 보상의 표본의 평균을 효율적으로 계산하는 방법이다.
행동의 가치 추정치 \(Q_n\)은 아래와 같다.
\[Q_n \doteq {R_1 + R_2 + ... + R_n \over n-1}\]이 식을 이용하여 행동 가치를 추정한다면, 표본을 생성할 때 마다 매 보상을 메모리에 저장해야한다. 이는 비효율적이다.
이 방법보다 더 효율적으로 같은 결과를 낼 수 있는 방법이 Incremental Implementation이다.
Incremental Implementation
새로 생성된 표본의 보상을 저장해서 매번 계산하는 방식이 아니라, 기존에 계산된 행동 가치 추정값을 Update하는 방식을 제안한다.
기존의 행동 가치 추정값을 Update(갱신)하는 방식을 사용하기 때문에 Incremental이라는 용어가 붙는다.
행동 가치 추정값인 \(Q_n\)과 n번째 새로 생성된 표본의 보상인 \(R_n\)만 주어지면 우리는 새로운 행동 가치 추정값인 \(Q_{n+1}\)을 계산할 수 있다.
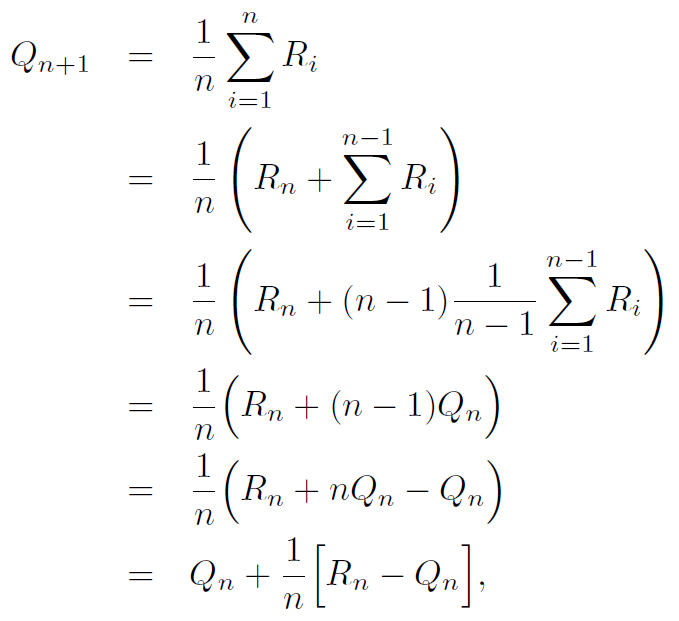
위 식의 의미는 아래와 같다.
\[NewEstimate \leftarrow OldEstimate + StepSize[Target-OldEstimate]\]\(Error = Target-OldEstimate\)이므로 Error에 StepSize를 고려해서 기존의 추정값에 Update하는 방식이다. 즉 추정값 \(Q_n\)과 보상값 \(R_n\)사이의 \(Error\)가 크면 그만큼 오차가 크다는 것을 의미하므로 많이 Update를 수행하고, 작으면 그만큼 오차가 적다는 것을 의미하므로 적게 Update를 수행한다.
여기에 \(StepSize\)는 표본 갯수에 반비례한다. 즉 도출된 추정값에 사용된 표본의 갯수에 따라 Update할 Error의 크기를 조절하는 것이다. 이를 통해 \(Q_n\)의 수렴을 유도할 수 있다.
Incremental Implementation을 이용한 Bandit algorithm의 Pseudocode는 아래와 같다.
