
Optimization & Loss Function
일반적으로 최적화를 위해서는 최적화 대상을 설정해야한다.
알고리즘에서는 참값과 예측값의 차이를 최적화 대상으로 선정하고 이를 Loss한다.
일반적으로 L1 loss와 L2 loss가 가장 잘 알려져있다.
L1 Loss는 아래와 같이 정의된다.
\[Loss(y,f(x))=\sum_{i=1}^N |y_{i}-f(x_{i})|\]L2 Loss는 아래와 같이 정의된다.
\[Loss(y,f(x))=\sum_{i=1}^N (y_{i}-f(x_{i}))^2\]두 방법 모두 장단점을 가지고있다.
L1 Loss의 경우, ‘V’자 형태로 미분 불가능한 지점이 있지만, 상대적으로 L2 Loss에 비해 Outlier에 의한 영향은 적다.
L2 Loss의 경우, ‘U’자 형태로 모든 지점에서 미분 가능하지만, Outlier의 Error가 제곱되므로 Outlier에 취약한 단점이 있다.
Huber Loss
Huber Loss는 L1과 L2의 장점을 취하면서 단점을 보완하기 위해서 제안된 것이 Huber Loss다.
위의 설명대로라면, Huber Loss는 모든 지점에서 미분이 가능하면서 Outlier Robust한 성격을 보여줘야한다.
Huber Loss의 정의는 아래와 같다.
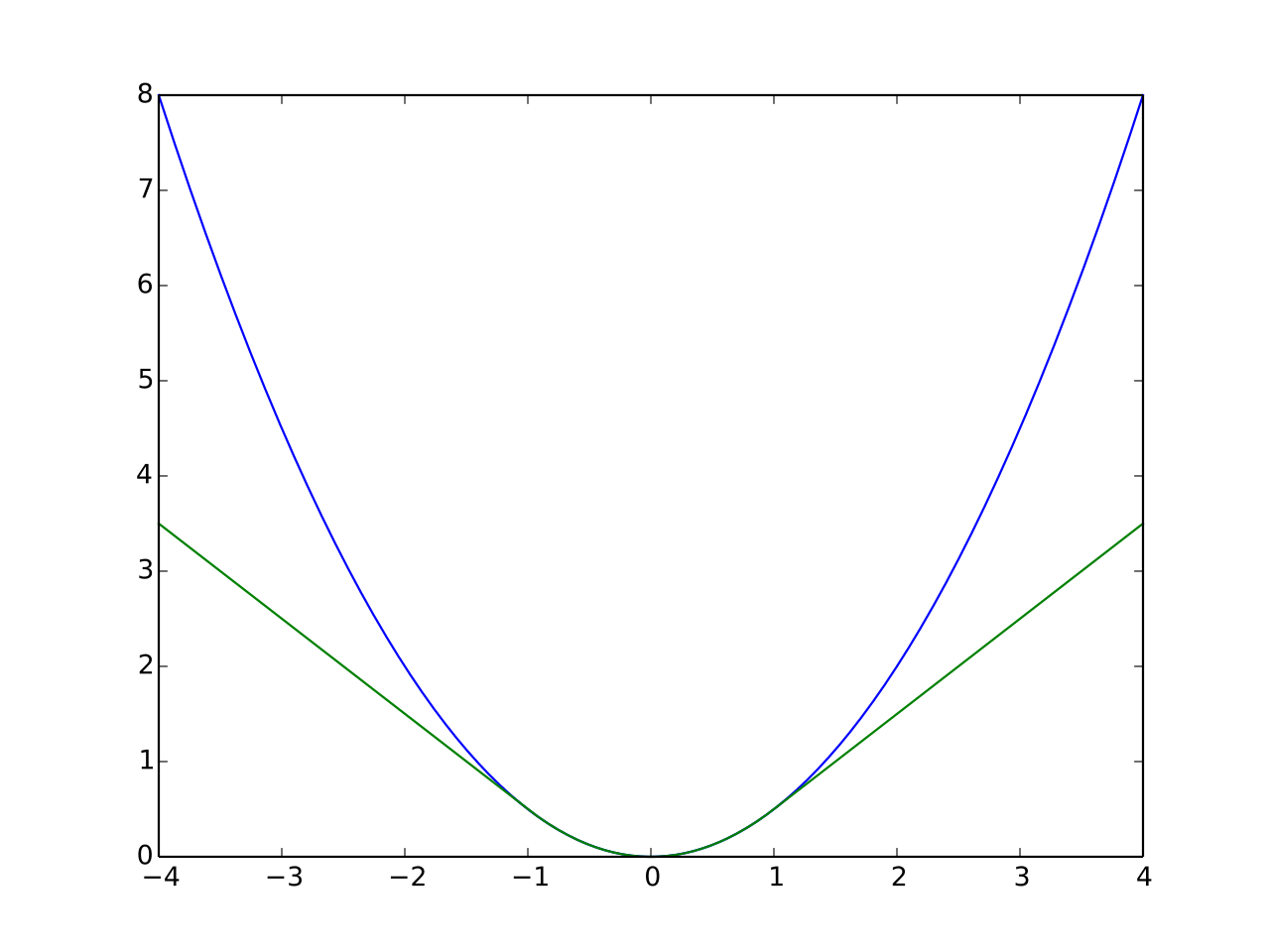
\[Loss_{\delta}(y,f(x))=\begin{cases}{1\over2}((y_{i}-f(x_{i}))^2 & for \left\vert y_{i}-f(x_{i}) \right\vert \le \delta, \\ \delta\left\vert y_{i}-f(x_{i}) \right\vert - {1\over2}\delta^2 & otherwise.\end{cases}\]아래의 그림은 𝛿를 1로 설정하였을 때의 Huber Loss(초록)와 L2 Loss(파랑)의 Loss다.
그림에서 확인할 수 있는 것처럼 -1과 1사이에서는 L2 Loss와 유사하며, 그 외의 영역에서는 L1 Loss와 유사한 형태를 보인다.
따라서 Huber Loss는 L1 Loss와 L2 Loss의 장점을 취한다.
- 모든 지점에서 미분이 가능하다.
- Outlier에 상대적으로 Robust하다.
Pytorch의 F.smooth_l1_loss()는 어떻게 계산될까?
아래 그림의 Loss를 계산하실 수 있다면 PASS!

Pytorch에서 Model Optimization할 때 사용하는 F.smooth_l1_loss()가 Huber Loss를 이용하여 Loss를 계산한다. 아래 그림은 Pytorch의 F.smooth_l1_loss의 description이다.
F.smooth_l1_loss에서는 𝛿를 1로 사용하는 것을 확인할 수 있다. 